一年级
小明今年7岁,当他13岁的时候,妈妈正好43岁。妈妈今年多少岁?
二年级
一列队伍中的人数比20多,比30少。按1、2、3、4报数,最后一人报3;按1、2、3报数,最后一人报2。这列队伍有多少人?
三年级
一桶油连桶共重52千克,把油倒掉一半后,剩下的油和桶重27千克。问:桶重多少千克?
四年级
抽屉里有若干个玻璃球,小军每次拿出其中的一半再放回1个,这样一共拿了5次,抽屉里还有3个玻璃球。原来抽屉里有多少个玻璃球?
五年级
23/30的分子和分母同时减去同一个数,约分后是3/4,同时减去的这个数是多少呢?
六年级
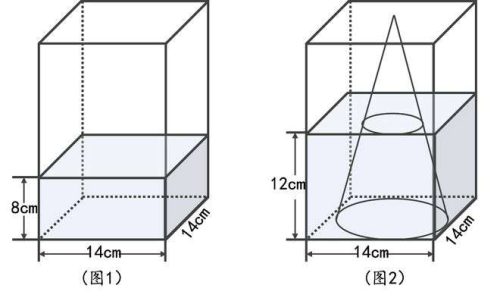
一个底面是正方形的容器里(如图1所示)装着水,从里面量底面边长是14cm,水的高度8cm,把一个铁质实心圆锥直立在容器里(如图2所示)后,水的高度上升到了12cm,刚好没过圆锥高的1/2,圆锥的底面积是多少?
请做完题之前不要看下面的答案!!独立思考很重要!切记!切记!切记!
答
一年级
【答案】妈妈今年37岁。
【解析】思路一:通过已知信息“小明今年7岁,当他13岁的时候,妈妈正好43岁”,可知小明13-7=6年后是13岁,那时妈妈正好是43岁,也就是说妈妈6年后43岁,因此妈妈今年43-6=37岁;思路二:通过已知信息“小明13岁的时候,妈妈正好43岁”,可知妈妈比小明大43-13=30岁,小明今年7岁,那妈妈今年就是7+30=37岁。
二年级
【答案】这列队伍有23人。
【解析】通过题目信息可知:按1、2、3、4报数,最后一人报3,就是每4人为一组,还余3。按1、2、3报数,最后一人报2,就是每3人为一组,余2。因为这一列队伍人数比20多,比30少,可以先想4×( )+3的结果在20~30之间,根据4的乘法口诀,符合的有4×5+3=23,4×6+3=27;再想3×( )+2的结果在20~30之间,根据3的口诀,符合的有3×7+2=23,3×8+2=26,3×9+2=29。两组都有的数是23,所以这列队伍有23人。
三年级
【答案】桶重2千克。
【解析】解决此类问题,要找到题中不变的量。把油桶里的油倒掉一半,桶的质量并没有变。所以,用原来油和桶的质量和减去剩下的油和桶的质量,得到的差就是半桶油的质量,即半桶油重:52-27=25(千克)。又因为桶中剩下的油也是半桶油,根据“剩下的油和桶重27千克”可以推出:用剩下的油和桶的质量减去半桶油的质量,即是桶的质量,所以桶重:27-25=2(千克)。
四年级
【答案】原来抽屉里有34个玻璃球。
【解析】此题可采用倒推法。由题意可知,“每次拿出其中的一半再放回1个”,也就是每次拿出其中的一半少1个。最后剩3个玻璃球,则第5次拿之前的玻璃球数为(3-1)×2=4(个),同理推出第4次拿之前的玻璃球数为(4-1)×2=6(个),第3次拿之前的玻璃球数为(6-1)×2=10(个),第2次拿之前的玻璃球数为(10-1)×2=18(个),第1次拿之前的玻璃球数为(18-1)×2=34(个)。
五年级

六年级
【答案】圆锥的底面积是112平方厘米。
【解析】方法一:原来水的体积:14×14×8=1568(立方厘米);放入圆锥后,圆锥没入水中那部分的体积和水的体积:14×14×12=2352(立方厘米);上升水的体积2352-1568=784(立方厘米),也就是圆锥没入水中那部分的体积。
又因为圆锥没入水中那部分的高12cm占整个圆锥高的1/2,因此整个圆锥的高为:12÷1/2=24cm。假设圆锥底面半径为r,则水上部分圆锥(高1/2处)的底面半径为r/2。
因此,整个圆锥的体积为:1/3×πr²×24,水上部分体积为:1/3×(r/2)²π×12,圆锥没入水中那部分体积为:
1/3×πr²×24-1/3×π(r/2)²×12=784
即:7πr²=784
解之,得πr²=112。所以,圆锥的底面积为112平方厘米。
方法二:根据题意可知,水上小圆锥的高与整个大圆锥的高的比为h1:h2=1:2;底面半径之比为r1:r2=1:2,因此底面积之比s1:s2=1:4;所以体积之比为v1:v2=1:8。由此推出圆锥没入水中那部分的体积占大圆锥体积的7/8。
又因为圆锥没入水中那部分的体积是784立方厘米(见方法一),因此整个圆锥的体积为784÷7/8=896(立方厘米),所以大圆锥的底面积为896×3÷(12×2)=112(平方厘米)。
素材来源网络,如涉及侵权,请联系删除!









发表评论