一元二次方程思维导图
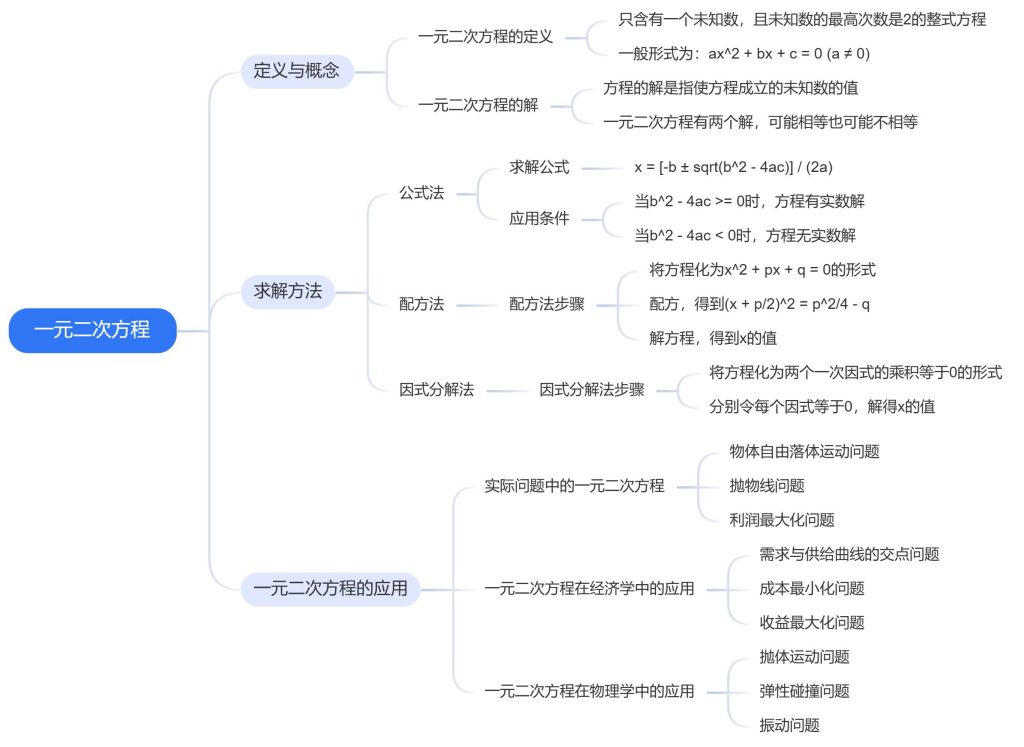
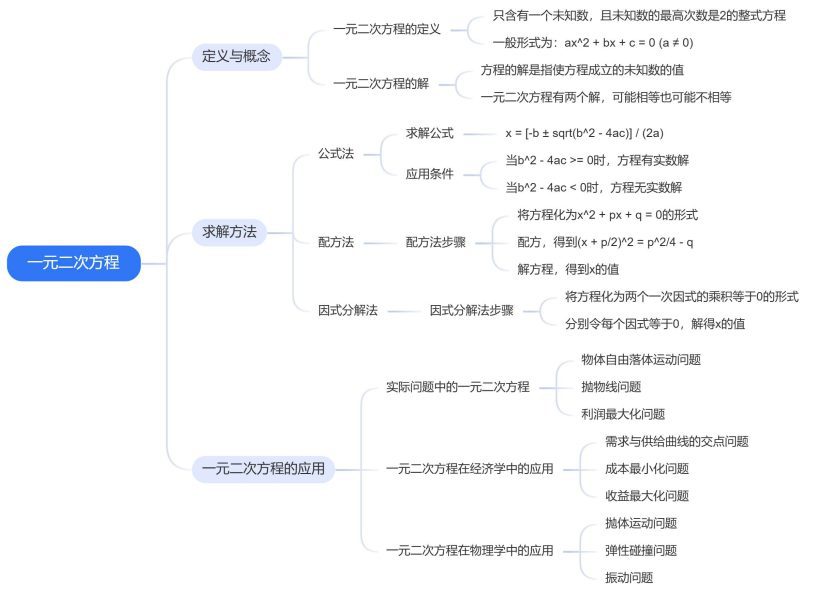
一元二次方程详解
一、定义与概念
一元二次方程是最基本也是最重要的代数方程之一。其一般形式为:
(ax^2 + bx + c 0)
其中,(a), (b), 和 (c) 是常数,且 (a ≠ 0)。在这个方程中,(x) 是未知数。
解:如果 (a), (b), 和 (c) 给定,使得该方程有解,那么这些解称为方程的根。
二、求解方法
- 公式法:对于任何一元二次方程,其解可以通过下面的公式得到:
(x \frac{b \pm \sqrt{b^2 4ac}}{2a})
这个公式是求解一元二次方程的基本工具,其中 (b^2 4ac) 称为判别式。 - 配方法:配方法是一种通过配方将一元二次方程转化为完全平方的形式,从而求解的方法。
- 因式分解法:如果一元二次方程可以因式分解为两个一次方程的乘积,那么就可以直接得到其解。例如,对于方程 (x^2 5x + 6 0),可以因式分解为 ((x2)(x3) 0),从而得到其解为 (x 2) 和 (x 3)。
三、一元二次方程的应用 - 实际问题中的一元二次方程:许多实际问题,如速度、距离和时间的关系,面积和长度的关系等,都可以通过建立一元二次方程来解决。
- 一元二次方程在经济学中的应用:在经济学中,一元二次方程常用于描述供需关系、成本分析等。例如,生产者可能会使用一元二次方程来确定最大化利润时的生产数量。
- 一元二次方程在物理学中的应用:在物理学中,一元二次方程常用于描述各种物理现象,如自由落体运动、弹性碰撞等。在这些情况下,方程可以表示物体的速度、加速度、位移等物理量之间的关系。
四、结论
一元二次方程不仅在数学本身中有着重要的地位,而且在经济学、物理学等实际领域也有着广泛的应用。通过理解一元二次方程的定义、概念和求解方法,我们不仅可以解决各种数学问题,而且可以应用这些知识和技能来解决实际问题。因此,学习和掌握一元二次方程是每个学生和研究人员都应该重视的任务。








发表评论