


勾股定理
一、定义与表述
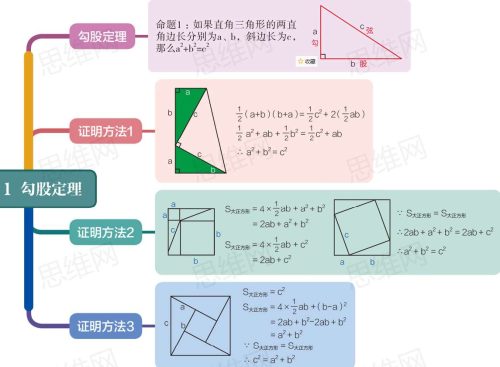
勾股定理,也称为毕达哥拉斯定理,是数学中一个基本且重要的定理。它表述了直角三角形两条直角边的平方和等于斜边的平方。具体来说,对于直角三角形ABC,其中角C为90度,边a和边b为直角边,斜边为c,则满足:
a^2 + b^2 c^2
二、勾股定理的证明
- 毕达哥拉斯证明法:根据毕达哥拉斯的证明,我们知道直角三角形三边的长度满足勾股定理。为了证明这一点,我们可以在直角三角形ABC中,以C为顶点,画一条穿过直角边BC且与斜边AC垂直的线段CD。由于CD垂直于BC,角BCD和角DCA都是90度。因此,三角形BCD和三角形ACD都是直角三角形。根据勾股定理,我们有:
b^2 CD^2 + BD^2
c^2 AD^2 + CD^2
a^2 AD^2 + BD^2
将上述三个等式相加,我们得到:
a^2 + b^2 c^2 - 欧几里得证明法:欧几里得使用反证法证明了勾股定理。假设不满足勾股定理,那么在直角三角形ABC中,我们可能有:
a^2 + b^2 ≠ c^2
但这将意味着三角形ABC不是直角三角形,这与题目条件矛盾。因此,我们的假设是错误的,所以勾股定理成立。
三、勾股定理的应用 - 数学领域:勾股定理在数学领域中有着广泛的应用。它常常用于解决与直角三角形相关的问题,例如求角度、长度等。同时,勾股定理也是三角函数和解析几何等领域的基础。
- 实际应用:勾股定理不仅在数学中有应用,在实际生活中也有很多应用。例如,建筑行业经常使用勾股定理来计算建筑物的角度和长度;航海中也常常使用勾股定理来计算航程和方位;在物理学中,勾股定理也常常被用来解决与力、运动和振动等相关的问题。
四、勾股定理的推广 - 勾股定理的逆定理:勾股定理的逆定理是勾股定理的一个重要推广。它表述了如果一个三角形的三边满足a^2 + b^2 c^2,那么这个三角形是一个直角三角形。这个逆定理常常被用来判断一个三角形是否为直角三角形。
- 勾股定理的推广形式:除了逆定理外,勾股定理还有其他的推广形式。例如,勾股定理可以推广到任意多边形的情况,包括四边形、五边形等。这些推广形式在解决实际问题中也有着广泛的应用。










发表评论