数列思维导图
数列:定义、类型及应用
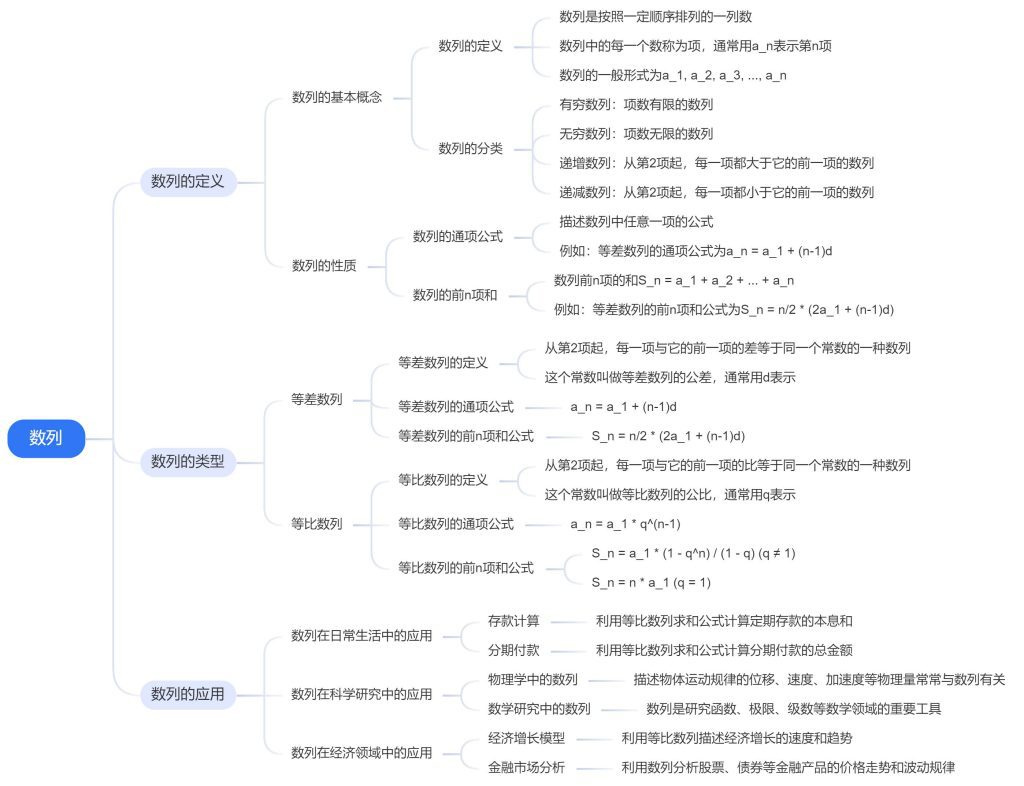
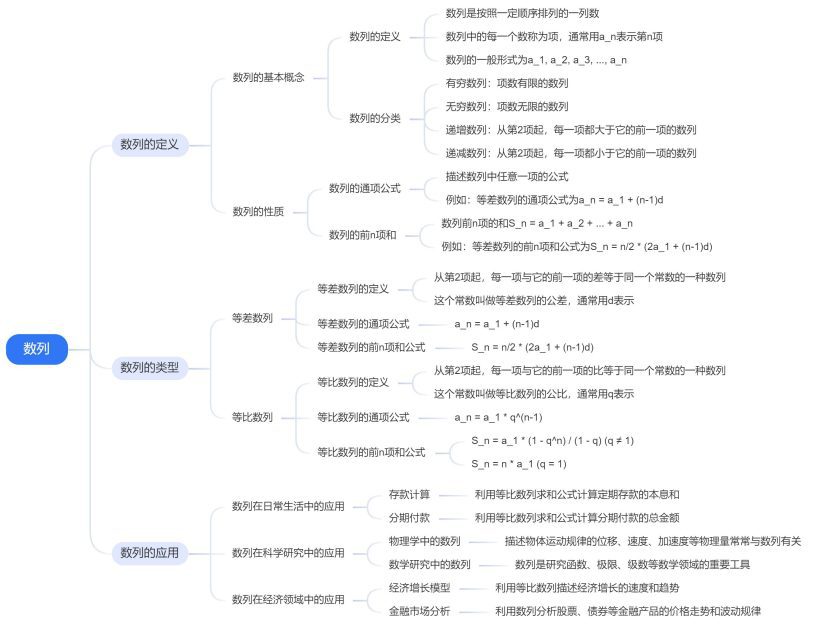
一、数列的定义
数列,作为数学中的一个基本概念,指的是按照某种特定顺序排列的一列数。这种顺序可以是按照自然数的递增,也可以是按照其他特定的规则。数列中的每一个数都被称为该数列的项,通常用a_n表示第n项。数列的每一项都与它的位置有关,位置的变化往往带来项值的变化。
数列的性质主要围绕其项之间的关系展开。例如,有些数列的相邻两项之间存在固定的差值,这样的数列被称为等差数列;而有些数列的相邻两项之间的比值是一个常数,这样的数列被称为等比数列。
二、数列的类型
- 等差数列:等差数列是一种最常见的数列类型,其特点是任意两项的差是一个常数,记作d。等差数列的通项公式为a_n a_1 + (n 1)d,其中a_1是首项,d是公差,n是项数。等差数列在日常生活中有很多应用,比如计算定期存款的本息和、预测物体的自由落体运动等。
- 等比数列:等比数列是另一种常见的数列类型,其特点是任意两项的比值是一个常数,记作r。等比数列的通项公式为a_n a_1 * r^(n1),其中a_1是首项,r是公比,n是项数。等比数列在科学研究、经济预测等领域有着广泛的应用,比如复利的计算、细菌繁殖的模拟等。
三、数列的应用 - 数列在日常生活中的应用:在我们的日常生活中,数列的应用非常广泛。比如,银行的定期存款就是一种等差数列的应用,每月存入固定的金额,到期后的本息和就是一个等差数列的和。此外,日常生活中的温度变化、物体下落等也都可以通过等差或等比数列进行模拟和预测。
- 数列在科学研究中的应用:在科学研究领域,数列同样扮演着重要的角色。比如,在物理学中,物体的振动频率、电磁波的波长等都可能形成等差或等比数列,通过这些数列的研究,科学家可以更深入地理解这些自然现象的本质。在生物学中,细菌繁殖的数量变化通常遵循等比数列的规律,这对于研究疾病的传播和防治有着重要的意义。
- 数列在经济领域中的应用:在经济领域中,数列的应用更是无处不在。比如,股票价格的涨跌、GDP的增长率等都可以看作是数列的应用。通过对这些数列的研究,经济学家可以预测未来的市场走势,为企业和政府的决策提供科学依据。此外,等比数列在复利计算中也有重要应用,这对于金融投资、保险等领域有着重要的实际意义。
综上所述,数列作为一种基础的数学概念,不仅在数学学科内部有着重要的地位,而且在日常生活、科学研究、经济领域等方面都有着广泛的应用。通过深入研究数列的性质和应用,我们可以更好地理解和解决现实世界中的各种问题。








发表评论