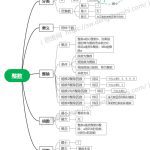
人教版六年级数学上册第一单元分数乘法思维导图
人教版六年级数学上册第一单元:分数乘法
一、引言
在六年级数学上册的第一单元中,我们将学习分数乘法这一重要概念。分数乘法不仅是数学基础的一部分,也是解决实际问题的有力工具。通过这一单元的学习,同学们将能够掌握分数乘法的定义、性质和运算方法,进而应用于生活实践之中。
二、分数乘法的定义与性质
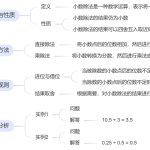
- 定义:分数乘法指的是两个分数相乘的运算。具体地,如果有两个分数a/b和c/d(b和d均不为0),那么它们的乘积为(a×c)/(b×d)。
- 性质:分数乘法满足交换律、结合律和分配律。即(a/b) × (c/d) (c/d) × (a/b);((a/b) × (c/d)) × (e/f) (a/b) × ((c/d) × (e/f));以及(a/b) × ((c/d) + (e/f)) (a/b) × (c/d) + (a/b) × (e/f)。
三、分数乘法的运算方法 - 分数与分数相乘:当两个分数相乘时,直接将它们的分子相乘,分母相乘。例如,(2/3) × (4/5) (2×4) / (3×5) 8/15。
- 分数与整数相乘:分数与整数相乘时,可以将整数视为分母为1的分数,然后进行运算。例如,3 × (2/5) (3/1) × (2/5) (3×2) / (1×5) 6/5。
四、分数乘法的应用 - 解决实际问题:分数乘法在实际生活中有着广泛的应用。比如,在分配任务或资源时,我们可能会用到分数乘法来计算每个人应得的部分。
- 分数乘法的拓展应用:在更高级的数学和物理课程中,分数乘法也扮演着重要角色。例如,在代数和几何中,我们经常需要用到分数乘法来解决复杂的问题。
五、分数乘法的练习 - 基础练习:通过大量的基础练习,同学们可以熟练掌握分数乘法的运算方法。这些练习可以包括简单的分数与分数相乘,以及分数与整数相乘的题目。
- 提高练习:在掌握了基础运算之后,同学们可以通过解决一些实际问题来进一步提高自己的分数乘法技能。这些问题可能会涉及到分数的加减乘除混合运算,需要同学们灵活运用所学的知识来解决。
六、结语
通过学习分数乘法,同学们不仅能够提高自己的数学技能,还能够更好地理解和应用数学知识于日常生活之中。希望大家能够认真学习,勤于练习,不断提高自己的数学水平。







发表评论