高中物理第十四章动量思维导图
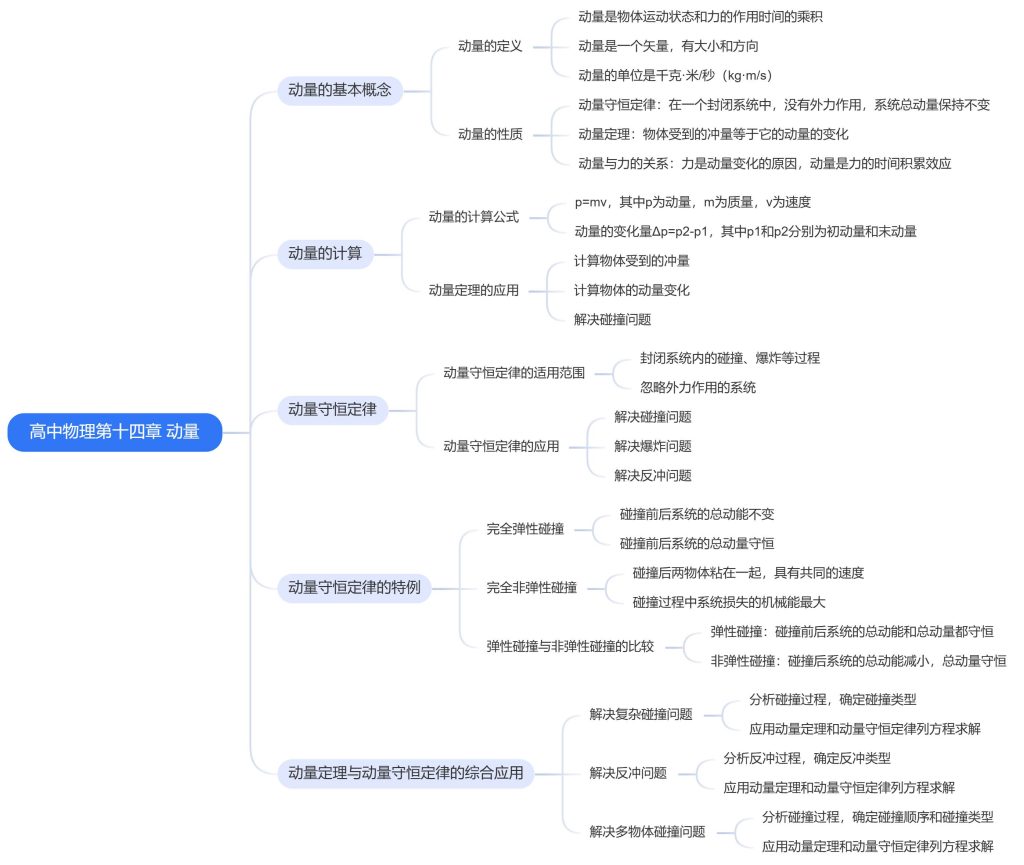
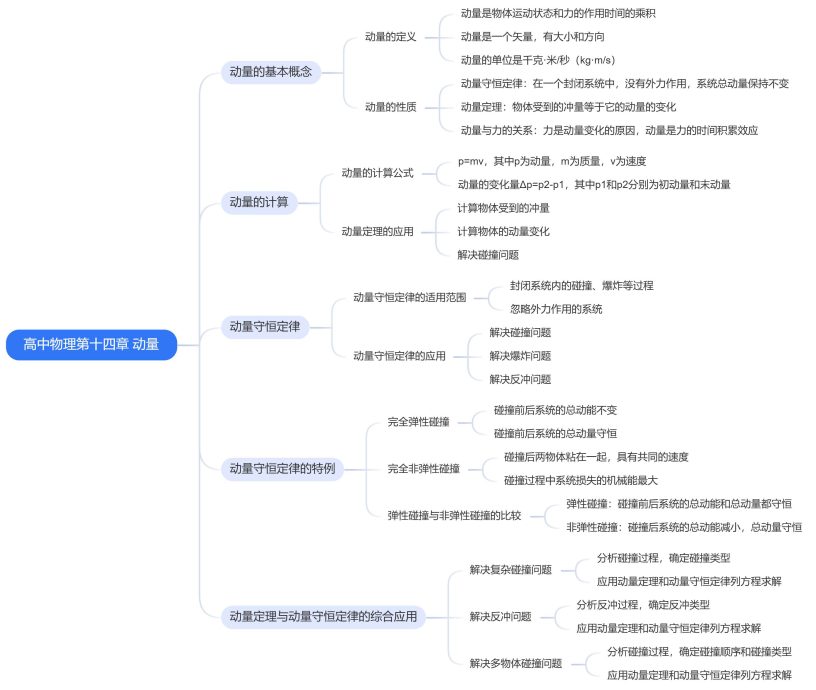
高中物理第十四章 动量
一、动量的基本概念
- 动量的定义
动量是描述物体运动状态的重要物理量,定义为物体的质量与速度的乘积,用符号p表示,数学公式为:p mv。其中,m表示物体的质量,v表示物体的速度。动量的方向与速度的方向相同。 - 动量的性质
(1)动量具有矢量性:动量既有大小,又有方向,是矢量。
(2)动量具有相对性:动量的值依赖于所选的参考系,不同参考系下动量的值可能不同。
(3)动量的守恒性:在不受外力或所受外力之和为零的系统中,系统的动量保持不变,即动量守恒。
二、动量的计算 - 动量的计算公式
动量的计算公式为p mv,其中m为物体的质量,v为物体的速度。注意,速度应为物体相对于同一参考系的速度。 - 动量定理的应用
动量定理表述为:合外力的冲量等于物体动量的变化,数学公式为:Ft Δp。通过动量定理,我们可以方便地解决一些涉及力、时间和速度变化的问题。
三、动量守恒定律 - 动量守恒定律的适用范围
动量守恒定律适用于系统不受外力或所受外力之和为零的情况。在实际问题中,当外力远小于内力,或者外力的作用时间远短于内力的作用时间时,也可以近似认为动量守恒。 - 动量守恒定律的应用
动量守恒定律在解决碰撞、爆炸等问题中具有广泛的应用。通过设定系统,分析系统的受力情况,判断动量是否守恒,再利用动量守恒定律列方程求解,是解决这类问题的基本方法。
四、动量守恒定律的特例 - 完全弹性碰撞
在完全弹性碰撞中,碰撞后物体的速度完全恢复,即碰撞过程中没有能量损失。完全弹性碰撞满足动量守恒和机械能守恒两个条件。 - 完全非弹性碰撞
在完全非弹性碰撞中,碰撞后两物体粘在一起,以同一速度运动。这种碰撞中,部分机械能转化为内能,系统机械能不守恒。 - 弹性碰撞与非弹性碰撞的比较
弹性碰撞和非弹性碰撞的主要区别在于能量损失的程度。弹性碰撞中能量损失为零,而非弹性碰撞中能量损失不为零。在实际生活中,非弹性碰撞更为常见。
五、动量定理与动量守恒定律的综合应用 - 解决复杂碰撞问题
在处理复杂碰撞问题时,需要综合考虑动量定理和动量守恒定律。首先分析系统的受力情况,判断动量是否守恒;然后利用动量定理或动量守恒定律列方程求解。 - 解决反冲问题
反冲问题是动量守恒定律的重要应用之一。在反冲问题中,一个物体在受到力的作用下发生运动,同时带动另一个物体向相反方向运动。通过设定系统并运用动量守恒定律,可以方便地解决这类问题。 - 解决多物体碰撞问题
在多物体碰撞问题中,需要分析每个物体的受力情况和运动状态,判断系统的动量是否守恒。然后,根据动量守恒定律列出方程组进行求解。这类问题通常较为复杂,需要较高的物理思维能力和解题技巧。
动量作为描述物体运动状态的重要物理量,在解决实际问题中具有广泛的应用。通过深入理解动量的基本概念、掌握动量的计算方法和动量守恒定律的应用,我们可以更好地理解和解决涉及动量的问题。同时,我们也要注意动量定理与动量守恒定律之间的联系和区别,灵活运用这两个定律解决复杂的物理问题。






发表评论